APPENDIX 2 EMPIRICAL BAYES ESTIMATION OF INDIGENOUS UNDERCOUNT
BACKGROUND
A2.1 Estimates of Indigenous undercount from the Census Post Enumeration Survey (PES) are required to adjust Census Indigenous figures as a key input to Indigenous estimated resident population (ERP). These estimates of Indigenous undercount adjustment should be stable (small standard errors) whilst minimising bias.
A2.2 Empirical Bayes (EB) estimation has been used by the ABS to estimate Indigenous undercount adjustments at state/territory by capital city/balance of state level - these are used to produce Indigenous ERP at state/territory level. These estimates and standard errors, prorated to ensure consistency with the Australian PES estimate, were directly produced from the EB estimator using Morris' algorithm (Morris 1983).
WHY THE EMPIRICAL BAYES APPROACH?
A2.3 High standard errors on the preliminary state/territory indigenous undercount rates lead to high sampling error for preliminary state/territory Indigenous ERP. The use of EB estimation in final rebasing in effect smoothed those parts of states with a high standard error, resulting in a more reliable undercount adjustment factor and final state/territory Indigenous ERP.
A MODEL FOR VARIATION OF UNDERCOUNT
A2.4 In estimating Indigenous numbers, the key item to be estimated from the PES is the "undercount adjustment", defined as the percentage increase to be applied to the Census count of Indigenous (after imputing for "not stated" Indigenous) to obtain a final Indigenous count. Suppose that the PES survey provides estimates 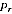 with variance
with variance 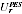 of undercount adjustment for each region r, where r indexes the 15 state/territory by capital city/balance of state regions. This provides information about the distribution of the true undercount adjustments
of undercount adjustment for each region r, where r indexes the 15 state/territory by capital city/balance of state regions. This provides information about the distribution of the true undercount adjustments 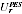 as follows.
as follows.
A2.1
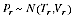
where this is read: "
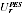
is distributed as a normal random variable with mean
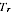
and variance
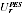
".
A2.5 This information is to be weighed up against a model for the likely actual variation between the true values. The information provided by this model is summarised as follows.
A2.2
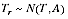
A2.6 This model says that, in the absence of survey information about individual regions, we would assume that the regions had similar values. The constant
A determines how different regions are likely to be in their undercount adjustments.
A2.7 A model like equation A2.2 was in fact the basis for the practice in 2001 of assuming that a single undercount adjustment should be applied to all regions. This was done in the light of the large survey error associated with PES estimates of Indigenous at state/territory level in 2001.
A2.8 Assuming first that the values
A and
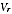
are known constants, and
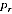
are provided from the PES survey. The best estimate of
T given equations A2.1 and A2.2 is given by:
A2.3
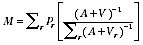
and the estimate of
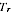
is:
A2.4
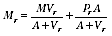
A2.9 This gives a very logical outcome: where variance
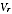
is high, the value
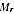
is very like the overall value
M,
while for a region with variance
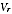
low the value
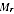
is close to the region's PES estimate
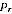
.
EMPIRICAL BAYES AND THE MORRIS ALGORITHM
A2.10 In the Empirical Bayes approach the survey estimates themselves are used to estimate the variability between the underlying true values i.e. to estimate the constant
A. The Morris algorithm gives a simple approach to this which should give a nearly optimal choice of
A.
A2.11 First, note that under the model, with
A known,
A2.5
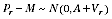
A2.12 Given this, set up the random variable
A2.6
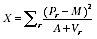
A2.13 This will have a chi-squared distribution with 14 degrees of freedom (there are 15 regions, but one degree of freedom is lost by substituting the estimator
M for the true value
T). The expected value of
X for this correct value of
A is then 14.
A2.14 The Morris algorithm proceeds to find the value
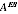
which when substituted for
A gives
X = 14. A simple iterative algorithm achieves this. This value is then used in producing estimates from equations A2.3 and A2.4.
STABLE VARIANCE PARAMETERS
A2.15 A first issue in applying the EB methodology is that the PES survey estimates of the variance
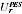
are quite unstable, being based on the same small sample of the Indigenous population as the PES estimates themselves. Rather than use these directly, the sample sizes in each region were used in apportioning each region a share of the overall variance.
A2.16 Suppose that the PES provided a simple random sample of size
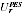
from the population (Indigenous and
non-Indigenous), with
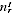
turning out to be Indigenous, of whom
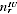
were undercounted. Writing
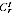
for the Indigenous
Census count,
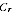
for the whole Census count and
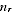
for the sample size, we have expected Indigenous sample
size of E(
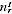
) =
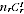
/
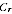
. Let the expected proportion undercounted be a constant
E(
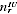
/
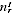
) =
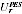
.
A2.17 The PES estimate
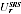
of undercounted Indigenous persons in region
r would then be:
A2.7
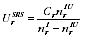
A2.18 Assuming that
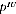
is small, we have:
A2.8
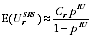
and:
A2.9
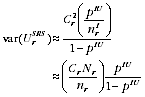
A2.19 In practice PES is not a simple random sample, nor is its estimator
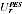
as simple as that above. The
above development is used to justify distributing the overall PES variance across Australia in proportion to
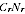
/
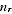
. Thus:
A2.10
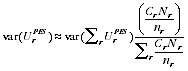
A2.20 Writing
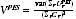
for the variance of the undercount adjustment at the Australia level, as estimated directly from the PES.
Noting that
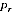
=
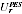
/
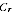
, the value
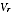
used in EB estimation is:
A2.11
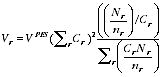
A2.21 Note that the resulting parameters
do not depend on the observed sample of the Indigenous
population in PES except via the overall variance estimate var(S
r 
).
ADJUSTING TO ADD TO THE AUSTRALIAN PES ESTIMATE
A2.22 The standard EB estimates are not guaranteed to add to the PES Indigenous estimate at Australia level. To enforce additivity to this PES estimate, a constant
c was added to the undercount adjustment rates in all regions. This gave the final estimates
A2.12
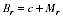
A2.23 Setting the constraint:
A2.13
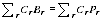
and writing
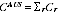
and
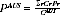
gives the value of
c as:
A2.14
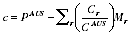
THE EB ESTIMATE AS A WEIGHTED AVERAGE OF PES REGION ESTIMATES
A2.24 Using an additive adjustment as given above to ensure additivity allows the EB estimates to be written as a simple weighted sum of the region PES estimates.
A2.15
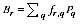
where:
A2.16
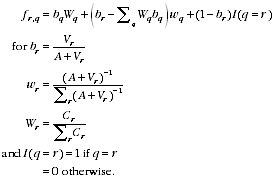
VARIANCE OF EB ESTIMATE CONDITIONAL ON A
A2.25 This and the next two sections give information about the reliability of the estimates conditional on a known value of
A. The effect of using the EB estimate of
A is discussed in a later section.
A2.26 Since the PES estimates for each region are almost independent, the variance of the empirical Bayes estimates follows from the linear form equation A2.15 as follows:
A2.17
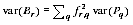
A2.27 The variance estimates var(
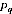
) are provided by the PES estimation system based upon the observed
data. They do not depend on the variance model that gave the values
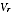
and are unbiased estimates of variance of the estimator (conditional on
A) whether or not the model given by equations A2.1 and A2.2 holds.
A2.28 Note also that state estimates can be written as a weighted sum of the component region estimates, and hence as a weighted sum similar to equation A2.15. The variance of a state estimate can thus be written in a form similar to equation A2.17.
EXPECTED BIAS UNDER THE MODEL
A2.29 Since the PES estimates are design-unbiased we have E(
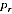
) =
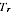
, and hence:
A2.18
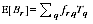
A2.30 Clearly if the true values
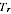
are treated as fixed unknown values with no underlying model, then the
estimate
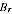
is biased to the extent that the particular region
r is different to other regions. So for a region with a
high value of
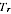
the estimate
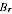
will tend to be biased downwards. However, for any actual region we do not know
the value of
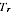
; we only observe the PES estimate
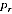
. A high value of
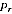
could be because
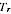
is high, or because the
sampling error was positive, or a combination of these. The estimate
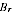
tries to balance these possibilities based on the model.
A2.31 The estimator
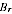
is unbiased for
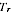
in the sense of expectation across repeated drawings from the model. Thus if we were able to repeatedly draw sets of 15 regions from the model (equation A2.2) and then get PES
estimates from them with variance structure given by equation A2.1, and use them to produce estimates
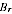
, then on average the bias would be zero. This is not very helpful, as even the overall mean estimate
M given by equation A2.3 is unbiased in this sense.
A2.32 More useful is to measure the mean squared bias (MSB) of the estimator (or its square root, the root mean squared bias or RMSB). The MSB is zero for the PES estimate, and
A for the mean estimate
M.
Writing E
M for expectation across the model, the MSB of
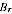
is obtained as follows:
A2.19
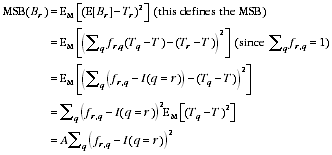
ESTIMATES OF MEAN SQUARED ERROR
A2.33 Adding the MSB (equation A2.19) to the variance (equation A2.17) gives the expected mean squared
error (MSE) of an EB estimate
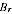
. The MSE serves as a summary of the likely size of errors from using the EB
estimator
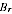
. Estimates of the root MSB (RMSB) and root MSE (RMSE) are presented in the following table, alongside SE of the PES and EB estimators.
A2.20 Estimates of SE, RMSB and RMSE for PES and EB estimates of undercount adjustment rate , States and territories |
|
 | PES | EB |
 | SE | RMSB | RMSE | SE(a) | RMSB | RMSE |
|
| New South Wales | 6.3 | - | 6.3 | 3.9 | 2.3 | 4.5 |
| Victoria | 9.9 | - | 9.9 | 3.1 | 4.1 | 5.1 |
| Queensland | 4.5 | - | 4.5 | 3.2 | 2.2 | 3.8 |
| South Australia | 10.0 | - | 10.0 | 3.3 | 3.9 | 5.1 |
| Western Australia | 8.8 | - | 8.8 | 4.2 | 2.9 | 5.1 |
| Tasmania | 7.8 | - | 7.8 | 2.9 | 3.9 | 4.9 |
| Northern Territory | 4.2 | - | 4.2 | 3.1 | 1.9 | 3.7 |
| Australian Capital Territory | 12.3 | - | 12.3 | 2.9 | 6.1 | 6.7 |
| Australia | 2.8 | - | 2.8 | 2.8 | - | 2.8 |
|
| - nil or rounded to zero (including null cells) |
| (a) The SE conditional on the EB value of A. |
A2.34 For a hypothetical region with no PES information at all, the RMSB would be sqrt(
A) = 6.6% and the RMSE would be 7.2% (larger because it still gets variance from the PES Australian estimate).
EFFECT OF ESTIMATING THE SMOOTHING CONSTANT A
A2.35 The estimator
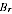
can be defined for any specified value of the ratio (
A /
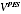
), and the resulting SEs can be predicted. These SEs do not depend on the model being correct at all (though the model is required for
analysis of the bias). Thus (
A /
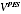
) could have been chosen to give estimates with a specified size of predicted
SEs. The Morris algorithm could still be used to estimate
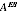
for presentation of RMSB etc.
A2.36 In 2006, the ABS has chosen to use the estimated value
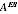
in defining the estimator
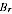
. Different estimates
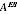
could have arisen, giving different estimates. Thus estimating
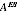
induces additional variability in the estimates.
A2.37 An example can make this clear. Suppose that a very unusual estimate arises by chance. This will
increase the estimated value
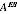
, which in turn will lead to the estimates being smoothed less than they should
be. Thus using the estimated
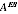
makes the estimates more subject to influence of unusual estimates i.e. more variable.
A2.38 In practice, the ABS is committed to presenting stable Indigenous ERP. In the future this may lead to
not using the estimated value
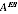
if it would lead to unstable estimates, or conversely an unnecessarily extreme smoothing.
A2.39 In the light of this, the ABS is content to present the SEs conditional on the chosen value
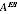
. Experimental estimates show that the unconditional SE of a "pure" EB estimate which always uses the
estimated
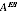
is somewhat increased over the SEs presented above. Even accounting for this, the unconditional RMSE will still be markedly lower than the SE of the PES estimates.
ALTERNATIVE MODELS AND ESTIMATORS
A2.40 It should be acknowledged that there are many alternative models that could have been used as the basis of an estimator, and alternative methods of producing the estimate. In the process of deciding to use Empirical Bayes techniques, a number of alternatives were investigated. These included modelling different classes of region (e.g. capital cities) separately, and looking for explanatory variables that could explain region differences. Different components of the undercount (e.g. the effect of misclassification as to whether a person is Indigenous) were also examined to see if predicting them separately could improve the estimator. The fit of these more sophisticated models was not sufficiently improved to justify choosing them over the simpler model (equation A2.2) that was used.
 Print Page
Print Page
 Print All
Print All