APPENDIX 2 SAMPLING VARIABILITY
INTRODUCTION
The estimates in this publication are based on information obtained from the occupants of a sample of dwellings. Therefore, the estimates are subject to sampling variability and may differ from the figures that would have been produced if information had been collected for all dwellings.
One measure of the likely uncertainty is given by the standard error (SE), which indicates the extent to which a sample might have varied compared to the population parameter because only a sample of dwellings was included. There are about two chances in three that the sample estimate will differ by less than one SE from the population parameter that would have been obtained if all dwellings had been enumerated, and about 19 chances in 20 that the difference will be less than two SEs. Another measure of the likely difference is the relative standard error (RSE), which is obtained by expressing the SE as a percentage of the estimate.
For estimates of population sizes, the size of the SE generally increases with the level of the estimate, so that the larger the estimate the larger the SE. However, the larger the sampling estimate the smaller the SE becomes in percentage terms (the RSE). Thus, larger sample estimates will be relatively more reliable than smaller estimates.
Estimates in this publication with RSEs of 25% or less are considered reliable for many purposes. Estimates with RSEs greater than 25% but less than or equal to 50% are annotated by an asterisk to indicate they are subject to high SEs and should be used with caution. Estimates with RSEs greater than 50%, annotated by a double asterisk, are considered too unreliable for general use and should only be used to aggregate with other estimates to provide derived estimates with RSEs of less than 50%.
RSEs for all tables are provided in the data cubes for this publication, which are available at the ABS website <www.abs.gov.au>. These can be accessed via the download tab for this publication. The RSEs have been derived using the delete-a-group jackknife method. If needed, SEs can be calculated using the estimates and RSEs.
COMPARATIVE ESTIMATES
Proportions and percentages
Proportions and percentages, which are formed from the ratio of two estimates, are also subject to sampling errors. The size of the error depends on the accuracy of both the numerator and the denominator. For proportions where the denominator is an estimate of the number of households in a grouping and the numerator is the number of households in a sub-group of the denominator group, the formula for an approximate RSE is given by:
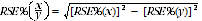
Differences between estimates
The difference between survey estimates is also subject to sampling variability. An approximate SE of the difference between two estimates (x-y) may be calculated by the formula:
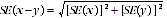
This approximation can generally be used whenever the estimates come from different samples, such as two estimates from different years or two estimates for two non-intersecting subpopulations in the one year. If the estimates come from two populations, one of which is a subpopulation of the other, the standard error is likely to be lower than that derived from this approximation.
SIGNIFICANCE TESTING
For comparing estimates between surveys, or between populations within a survey, it is useful to determine whether differences are 'real' differences between the corresponding population characteristics or simply the result of sampling variability between the survey samples. One way to examine this is to determine whether the difference between the estimates is statistically significant. This is done by calculating the standard error of the difference between two estimates (x and y), using the formula above, and using that to calculate the test statistic using the formula below:
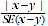
If the value of this test statistic is greater than 1.96 then there is good evidence of a statistically significant difference between the two populations with respect to that characteristic. Otherwise, it cannot be stated with confidence that there is a real difference between the population estimates.
 Print Page
Print Page
 Print All
Print All