|
|
TECHNICAL NOTE - SAMPLING VARIABILITY
MEASURING SAMPLING VARIABILITY
1. Since the estimates in this publication are based on information obtained from occupants of a sample of dwellings, they are subject to sampling variability, that is, they may differ from those that would have been produced if all dwellings had been included in the survey. One measure of the likely difference is given by the standard error (SE), which indicates the extent to which an estimate might have varied by chance because only a sample of dwellings was included. There are about two chances in three that a sample estimate will differ by less than one SE from the number that would have been obtained if all dwellings had been included, and about 19 chances in 20 that the difference will be less than two SEs. Another measure of the likely difference is the relative standard error (RSE), which is obtained by expressing the SE as a percentage of the estimate.
2. A table of SEs and RSEs for estimates of numbers of persons included in this publication appears at the end of this Technical note. These values do not give a precise measure of the SE or RSE for a particular estimate but will provide an indication of its magnitude.
CALCULATION OF STANDARD ERRORS
3. An example of the calculation and the use of SEs in relation to estimates of persons is as follows. Consider the estimate for Australia of pre-retired persons with no superannuation, which is 2,836,200. Since this estimate is between 2,000,000 and 5,000,000 in the SE table, the SE for the estimate will be between 30,580 and 45,310 and can be approximated by interpolation as 34,700 (rounded to the nearest 100). Therefore, there are about two chances in three that the value that would have been produced if all dwellings had been included in the survey will fall within 34,700 persons of the survey estimate, i.e. in the range 2,801,500 to 2,870,900, and about 19 chances in 20 that the value will fall within 69,400 persons of the survey estimate, i.e. in the range 2,766,800 to 2,905,600. This example is illustrated in the diagram below.
 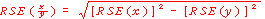 8. Consider the example above of the number of pre-retired persons with no superannuation (2,836,200). Of these, 1,304,400 or 46.0% were estimated to be male. The SE of 2,836,200 is approximately 34,700 so the RSE is 1.2%. The RSE for 1,304,400 is 1.9%. Applying the formula above, the RSE of the proportion is 1.5% giving a SE for the proportion (46.0%) of 0.68 percentage points. Therefore there are about two chances in three that the proportion of pre-retired persons with no superannuation who were male is between 45.3% and 46.7% and 19 chances in 20 the proportion is within the range 44.6% and 47.4%
9. Published estimates may also be used to calculate the difference between two survey estimates (numbers or percentages). Such an estimate is subject to sampling error. The sampling error of the difference between the two estimates depends on their SEs and the relationship (correlation) between them. An approximate SE of the difference between two estimates (x-y) may be calculated by the following formula:
8. Consider the example above of the number of pre-retired persons with no superannuation (2,836,200). Of these, 1,304,400 or 46.0% were estimated to be male. The SE of 2,836,200 is approximately 34,700 so the RSE is 1.2%. The RSE for 1,304,400 is 1.9%. Applying the formula above, the RSE of the proportion is 1.5% giving a SE for the proportion (46.0%) of 0.68 percentage points. Therefore there are about two chances in three that the proportion of pre-retired persons with no superannuation who were male is between 45.3% and 46.7% and 19 chances in 20 the proportion is within the range 44.6% and 47.4%
9. Published estimates may also be used to calculate the difference between two survey estimates (numbers or percentages). Such an estimate is subject to sampling error. The sampling error of the difference between the two estimates depends on their SEs and the relationship (correlation) between them. An approximate SE of the difference between two estimates (x-y) may be calculated by the following formula:
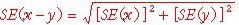 10. While this formula will be exact only for differences between separate and uncorrelated characteristics of subpopulations, it is expected to provide a good approximation for all differences likely to be of interest in this publication.
11. The imprecision due to sampling variability, which is measured by the SE, should not be confused with inaccuracies that may occur because of imperfections in reporting by interviewers and respondents and errors made in coding and processing data. Inaccuracies of this kind are referred to as non-sampling error and they may occur in any enumeration, whether it be a full count or a sample.
10. While this formula will be exact only for differences between separate and uncorrelated characteristics of subpopulations, it is expected to provide a good approximation for all differences likely to be of interest in this publication.
11. The imprecision due to sampling variability, which is measured by the SE, should not be confused with inaccuracies that may occur because of imperfections in reporting by interviewers and respondents and errors made in coding and processing data. Inaccuracies of this kind are referred to as non-sampling error and they may occur in any enumeration, whether it be a full count or a sample.
STANDARD ERRORS OF ESTIMATES
|
 | Standard Error
| Australia
|
Size of estimate (persons) | NSW | Vic. | Qld | SA | WA | Tas. | NT | ACT | Standard error | Relative standard error |
 | no. | no. | no. | no. | no. | no. | no. | no. | no. | % |
|
400 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 230 | 460 | 115 |
500 | 0 | 0 | 0 | 0 | 0 | 320 | 0 | 260 | 520 | 104 |
600 | 0 | 0 | 0 | 0 | 0 | 350 | 400 | 290 | 570 | 95 |
700 | 0 | 0 | 0 | 0 | 0 | 370 | 430 | 310 | 620 | 89 |
800 | 0 | 0 | 0 | 0 | 0 | 400 | 460 | 330 | 670 | 84 |
900 | 0 | 0 | 0 | 0 | 0 | 420 | 480 | 350 | 710 | 79 |
1,000 | 0 | 0 | 0 | 0 | 0 | 440 | 510 | 370 | 750 | 75 |
1,100 | 0 | 0 | 0 | 0 | 0 | 460 | 530 | 390 | 790 | 72 |
1,200 | 0 | 0 | 0 | 650 | 700 | 480 | 550 | 410 | 830 | 69 |
1,300 | 0 | 0 | 0 | 680 | 730 | 500 | 570 | 420 | 870 | 67 |
1,400 | 0 | 0 | 0 | 710 | 760 | 520 | 590 | 440 | 900 | 64 |
1,500 | 0 | 0 | 0 | 730 | 780 | 530 | 610 | 460 | 940 | 63 |
1,600 | 0 | 0 | 950 | 760 | 810 | 550 | 620 | 470 | 970 | 61 |
1,700 | 0 | 0 | 980 | 780 | 840 | 570 | 640 | 480 | 1,000 | 59 |
1,800 | 0 | 1,080 | 1,010 | 800 | 860 | 580 | 660 | 500 | 1,030 | 57 |
1,900 | 0 | 1,110 | 1,030 | 830 | 890 | 600 | 670 | 510 | 1,060 | 56 |
2,000 | 0 | 1,140 | 1,060 | 850 | 910 | 610 | 690 | 520 | 1,090 | 55 |
2,100 | 0 | 1,170 | 1,090 | 870 | 930 | 630 | 700 | 530 | 1,120 | 53 |
2,200 | 0 | 1,200 | 1,120 | 890 | 960 | 640 | 720 | 550 | 1,150 | 52 |
2,300 | 0 | 1,230 | 1,140 | 910 | 980 | 660 | 730 | 560 | 1,170 | 51 |
2,400 | 0 | 1,250 | 1,170 | 930 | 1,000 | 670 | 750 | 570 | 1,200 | 50 |
2,500 | 1,440 | 1,280 | 1,190 | 950 | 1,020 | 680 | 760 | 580 | 1,230 | 49 |
3,000 | 1,580 | 1,410 | 1,310 | 1,040 | 1,120 | 740 | 830 | 630 | 1,350 | 45 |
3,500 | 1,710 | 1,530 | 1,420 | 1,120 | 1,210 | 800 | 880 | 680 | 1,460 | 42 |
4,000 | 1,830 | 1,640 | 1,520 | 1,200 | 1,300 | 850 | 940 | 720 | 1,570 | 39 |
4,500 | 1,940 | 1,740 | 1,620 | 1,270 | 1,370 | 900 | 990 | 760 | 1,670 | 37 |
5,000 | 2,050 | 1,840 | 1,710 | 1,340 | 1,450 | 950 | 1,040 | 800 | 1,760 | 35 |
6,000 | 2,240 | 2,020 | 1,870 | 1,460 | 1,590 | 1,040 | 1,120 | 860 | 1,940 | 32 |
8,000 | 2,590 | 2,330 | 2,160 | 1,680 | 1,830 | 1,190 | 1,280 | 980 | 2,240 | 28 |
10,000 | 2,890 | 2,600 | 2,420 | 1,860 | 2,040 | 1,320 | 1,410 | 1,080 | 2,510 | 25 |
20,000 | 4,050 | 3,650 | 3,400 | 2,560 | 2,860 | 1,840 | 1,920 | 1,430 | 3,560 | 18 |
30,000 | 4,930 | 4,420 | 4,140 | 3,070 | 3,470 | 2,230 | 2,300 | 1,680 | 4,360 | 15 |
40,000 | 5,650 | 5,050 | 4,760 | 3,480 | 3,980 | 2,560 | 2,620 | 1,880 | 5,020 | 13 |
50,000 | 6,280 | 5,590 | 5,290 | 3,840 | 4,420 | 2,850 | 2,890 | 2,040 | 5,590 | 11 |
100,000 | 8,700 | 7,630 | 7,320 | 5,130 | 6,080 | 3,970 | 3,940 | 2,610 | 7,810 | 8 |
200,000 | 11,970 | 10,300 | 10,070 | 6,790 | 8,310 | 5,530 | 5,360 | 3,300 | 10,820 | 5 |
300,000 | 14,400 | 12,200 | 12,090 | 7,960 | 9,950 | 6,710 | 0 | 3,750 | 13,070 | 4 |
400,000 | 16,390 | 13,740 | 13,740 | 8,880 | 11,280 | 7,700 | 0 | 0 | 14,910 | 4 |
500,000 | 18,120 | 15,040 | 15,160 | 9,660 | 12,430 | 0 | 0 | 0 | 16,510 | 3 |
1,000,000 | 24,620 | 19,760 | 20,490 | 12,440 | 16,700 | 0 | 0 | 0 | 22,540 | 2 |
2,000,000 | 33,280 | 25,680 | 27,490 | 15,830 | 22,280 | 0 | 0 | 0 | 30,580 | 2 |
5,000,000 | 49,130 | 35,680 | 40,100 | 0 | 0 | 0 | 0 | 0 | 45,310 | 1 |
10,000,000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 60,540 | 1 |
15,000,000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 71,500 | 0 |
|
ESTIMATES WITH RELATIVE STANDARD ERRORS OF 25% AND 50%
|
Size of estimate (persons) | NSW | Vic. | Qld | SA | WA | Tas. | NT | ACT | Aust. |
 | no. | no. | no. | no. | no. | no. | no. | no. | no. |
|
Estimates with RSEs of 25% | 13277 | 10825 | 9356 | 5705 | 6718 | 2956 | 3566 | 2175 | 10115 |
Estimates with RSEs of 50% | 3348 | 2638 | 2272 | 1429 | 1643 | 784 | 1022 | 551 | 2405 |
|
 Print Page
Print Page
 Print All
Print All