|
|
TECHNICAL NOTE: SAMPLING VARIABILITY
ESTIMATION PROCEDURE
1. Estimates derived from this survey were obtained in two stages. In the first stage the effects of non-response were investigated by analysing the demographic composition of the Monthly Population Survey sample and response patterns to the Crime and Safety Survey after reminder action had been undertaken. This information was used to determine the appropriate adjustment procedure for non-response.
2. The second stage was a complex ratio estimation procedure. This procedure ensured that the survey estimates for persons conformed to independent estimates of the population, commonly referred to as 'benchmarks', rather than to the distribution of demographic characteristics among the survey respondents. These benchmarks consist of population estimates by age, sex, and part of state. A similar procedure also ensured that household estimates conformed to independent estimates of households by number of adults, number of children in the household and part of state.
3. Since the 2004 Crime and Safety Survey, the process for producing household benchmarks has been revised. A paper describing these changes in detail is currently being developed and is due for release in early 2007 (cat. no. 3107.0.55.007).
RELIABILITY OF ESTIMATES
4. Estimates in this publication are subject to non-sampling and sampling errors.
Non-sampling errors
5. Non-sampling errors may arise as a result of errors in the reporting, recording or processing of the data and can occur even if there is a complete enumeration of the population. Non-sampling errors can be introduced through inadequacies in the questionnaire, non-response, inaccurate reporting by respondents, errors in the application of survey procedures, incorrect recording of answers and errors in data entry and processing.
6. It is difficult to measure the size of the non-sampling errors. The extent of these errors could vary considerably from survey to survey and from question to question. Every effort is made to minimise reporting error by the careful design of questionnaires, intensive training and supervision of staff, and efficient data processing procedures.
Sampling errors
7. Sampling errors are the errors which occur by chance because the data was obtained from a sample, rather than from the entire population.
ESTIMATES OF SAMPLING ERROR
8. One measure of the variability of estimates which occurs as a result of surveying only a sample of the population is the standard error (see table below).
9. There are about 2 chances in 3 (67%) that a sample estimate will differ by less than one standard error from the number that would have been obtained if all dwellings had been included, and about 19 chances in 20 (95%) that the difference will be less than two standard errors.
10. Linear interpolation is used to calculate the standard error of estimates falling between the sizes of estimates listed in the table.
11. The standard error (SE) can also be expressed as a percentage of the estimate. This is known as the relative standard error (RSE). The relative standard error is determined by dividing the standard error of an estimate SE(x) by the estimate x and expressing it as a percentage. That is—(where x is the estimate)
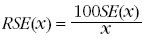
12. An example of the calculation and use of standard errors for estimates of households follows. Table 1 shows that the estimated number of households in NSW that have been a victim of motor vehicle theft is 26,200. Since the estimate is between 20,000 and 30,000 the standard error (as shown in the table below) will be between 3,650 and 4,316 and can be approximated as 4,100 (by linear interpolation). Thus there are about 2 chances in 3 that the value that would have been obtained, had all dwellings been included in the survey, lies between 22,100 and 30,300. Similarly, there are about 19 chances in 20 that the value lies between 18,000 and 34,400.
13. Proportions and percentages formed from the ratio of two estimates are also subject to sampling error. This size of the error depends on the accuracy of both the numerator and the denominator. The formula for the relative standard error (RSE) of a proportion or percentage is—
![Equation - RSE(x/y)= square root of [RSE(x)] squared - [RSE(y)] squared](/AUSSTATS/abs@.nsf/7d12b0f6763c78caca257061001cc588/068b4f0aff244781ca25739500186098/Body/0.1D62!OpenElement&FieldElemFormat=gif)
14. Only estimates with relative standard errors of 25% or less, and percentages based on such estimates, are considered sufficiently reliable for most purposes. However, estimates and percentages with a larger RSE have been included, preceded by * (RSE between 25% and 50%) or ** (RSE greater than 50%) to indicate that they are subject to high standard errors and should be used with caution.
STANDARD ERRORS OF ESTIMATES OF HOUSEHOLDS AND PERSONS, April 2006
Size of estimate | Standard error | Relative standard error |
|
(households and persons) | no. | % |
1,000 | 732 | 73.2 |
1,500 | 944 | 63.0 |
2,000 | 1,124 | 56.2 |
2,500 | 1,281 | 51.2 |
3,000 | 1,422 | 47.4 |
3,500 | 1,550 | 44.3 |
4,000 | 1,668 | 41.7 |
5,000 | 1,880 | 37.6 |
8,000 | 2,391 | 29.9 |
10,000 | 2,665 | 26.7 |
20,000 | 3,650 | 18.2 |
30,000 | 4,316 | 14.4 |
50,000 | 5,243 | 10.5 |
100,000 | 6,625 | 6.6 |
200,000 | 8,086 | 4.0 |
300,000 | 8,941 | 3.0 |
500,000 | 9,978 | 2.0 |
1,000,000 | 11,238 | 1.1 |
2,000,000 | 12,225 | 0.6 |
3,000,000 | 12,637 | 0.4 |
4,000,000 | 12,846 | 0.3 |
|
STATISTICAL SIGNIFICANCE TESTING
15. Where differences between data items have been noted in the Summary of Findings, they are statistically significant unless otherwise specified. In this publication a statistically significant difference is one where there are 19 chances in 20 that the difference noted reflects a true difference between population groups of interest rather than being the result of sampling variability.
16. In tables 1, 2, 3, 4, 6 and 8 of this publication, apparent changes in results between the 2006 survey and previous NSW Crime and Safety surveys have been tested to determine whether the changes are statistically significant. That is, to determine whether it is likely that the differences observed in sample estimates indicate real differences in the population. In these tables, cells which have not changed significantly over time are indicated. In other tables, which do not show the results of significance testing, users should take account of RSEs when comparing estimates for different populations.
|
|
 Print Page
Print Page
 Print All
Print All